It might be noted that the above Surface Elements are sufficient to describe a low-dimensional surface, such as the typical earth surface where gradients do not exceed 90˚. The typology would be insufficient to fully describe high-relief terrain features such as overhanging ledges, caves, arches and manmade surfaces whose gradients exceed 90˚. Perhaps each of the six Surface Elements has an inverse "negative element" that describes the surface of >90˚ "upside-down" surfaces.
3.2. The Surface Network
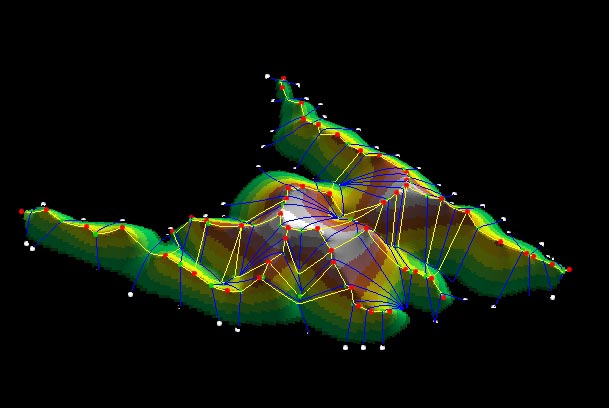
Surface networks are data structures that abstract topological surfaces, such as the earth's surface, by storing only the critical points and lines of that surface (Rana). Wood (1996) and others developed a way to model landforms by essentially removing the slope points from the digital elevation data. This allows terrain to be modeled and manipulated with very few data points.
Figure 1: COMPUTER
GENERATED MODEL OF A
SURFACE NETWORK
image courtesy of
Sanjay Rana
 Many of the developments in this
field over the past twenty years have focused on the development of
computer
automated detection from DEMs, TINs and other digital data
sources. Rana
(2002) gives an excellent history on the development of Surface
Networks, going
back to Cayley and Maxwell. [16]
Surface Networks are useful to our
purposes of developing a prominence-derived model of summits because
they describe
the super-structure into which saddles, summits and ridges fit.
Many of the developments in this
field over the past twenty years have focused on the development of
computer
automated detection from DEMs, TINs and other digital data
sources. Rana
(2002) gives an excellent history on the development of Surface
Networks, going
back to Cayley and Maxwell. [16]
Surface Networks are useful to our
purposes of developing a prominence-derived model of summits because
they describe
the super-structure into which saddles, summits and ridges fit.
A Surface Network is in fact two separate and interlocking networks. Mark (1988) refers to these as Channel Networks and Ridge Networks.
Channels and pits form one kind of network. Practically speaking, this is the hydrological network of streams, rivers and lakes that comprise drainage basins. Their form, a classic dendritic tree, has been well studied by mathematicians and hydrologists.
The Ridge Network, composed of summit, saddle and ridge elements is much less well described in the earth science literature, though its mathematical form is known in Morse topology. The Ridge Network forms the delimitations of all drainage basins. A continent or island is composed of one central ridge network, and many channel networks that radiate out from the ridge network like petals. The two networks touch at infinite points (scale independent) but never cross.
3.3.
Maxwell's
Hills and
Dales
3.4. Ridge and Channel Networks
What Maxwell and
Morse developed
mathematically, we may derive independently as a function of mountain
prominence: That every summit
(except the highest one) corresponds to a saddle. (Every pit also
corresponds to another kind of saddle that we will discuss
below.) Prominence Theory
demonstrates that each summit:saddle and pit:saddle pair is unique and
has a
specific
geolocation.
Ridges and channels are special kinds of slope lines. They also can be "coupled"; as two unique pairs of slope lines eminating from a saddle. Every saddle (both key and basin) has one unique ridge line and one unique channel line. One pair of slope lines ascend on opposite sides from the saddle to form two ridge lines that each terminate at a point of local maximum, a summit. The other pair of slope lines descends on opposite sides from the saddle to form two channel lines that each terminate at another channel line or at a point of local minimum. Most slope lines reach a point of local minimum. In fact certain kinds of ridges are the only kind of slope line that never reach a point of local minimum, i.e. a channel, pit, or sea level.
Ridges correspond to points of maximum curvature of contour lines. Morphometrically, ridges can be demonstrated to be one of two forms. Ridges that connect summits and saddles, and therefore always terminate in a summit, can be described as Crests. Other ridges, including an infinite number of minor ones, do not terminate at a summit but rather terminate (or more precisely become indistinguishable from slope) at a point of local minimum; a channel, pit or flat-body of water. They can be described as Spur ridges (my definitions). The distinction between crests and spurs is not important in Surface Network theory but it is elemental to the study of summits. By eliminating spurs from a Ridge Network we thereby greatly simplify the tree to a structure that connects only summits and saddles. I call this simplified network a Divide Tree.
Channels are
points of maximum curvature of
contour
lines. Morphometrically, they all
take the same relative form, although the field of hydrology describes
a
hierarchical ordering of channels.
Channels are a particular kind of slope line.
Slope lines descend from all points along a Ridge Network,
i.e. summits, saddles, and crest and spur ridges. Slope
lines always merge at a channel or pit. A
channel can be said to be formed at both a. saddles and b. wherever at
least
two slope lines merge.
Stream-ordering is a qualitative analysis of specifically fluvial channels based on a dendritic drainage pattern. A first-order stream is a primary watercourse with few, if any branches, a second order stream is formed by the junction of two first-order streams and so on. While this analysis is useful to hydrology, it is not necessarily analogous to a morphometric ordering of channels (i.e. channels which take the same morphological form whether or not there is water in them.)
I propose that there is a similar morphometric distinction for channels as there is for ridges. Channels that originate at saddles are unique slope lines that form the natural division of hills. All other channels form at the junction of any two generic slope lines that descend from any point on the Ridge Network.
3.5 Key Saddles and Basin Saddles
Every saddle that corresponds to a summit can be termed a key saddle. Similarly, saddles that correspond to a depression or pit are termed Basin Saddles. Basin saddles (Cayley called these Bars) take the same physical form as key saddles, but serve a different morphometric function.
A pit is the lowest point of a depression. Every pit is circumscribed by an enclosing ridgeline. We call the area inside that ridgeline an Enclosed Basin.[17] The basin saddle is the lowest point on that ridgeline, which morphometrically is of the same form as other saddles. The basin saddle is the point at which, if the pit were to fill with water, the new lake would overflow and spill into the adjoining drainage. The shape of this lake, i.e. the closed contour inside the enclosed basin, is the shape of the Depression, of which the pit is the lowest point.
The number of summits along an enclosing ridgeline is equal to the number of saddles, one of which is a basin saddle. As a basin saddle does not correspond to a summit, at least one summit along the ridgeline must have a key saddle that is off the ridgeline, or it must be the high point of the island or continent.