Section 5:

Distribution and Probability of Prominence

How is prominence distributed?  Can prominence be predictive?  How many mountains are there in the world? 

5.1        Persistence of prominence in the United States

In my research, I identified 1,234 mountains in the Lower 48 United States with a possible prominence of 2,000'.  The dataset includes 1,193 peaks with "clean" prominence, and 41 peaks in the "error range".   The completion of a clean dataset to a given prominence cutoff value gives us the opportunity to observe distribution and probability trends for mountains in general.

All mountains have an exact prominence value.  In practice however, summits are usually assigned a range of possible values.  This is because USGS topographic maps, which generally provide benchmark or spot elevations for major summits, rarely provide spot elevations for saddles.  Therefore P values can be expressed in an "error range" that generally represents the one contour interval uncertainty of the exact saddle elevation.

U.S. prominence is not surprisingly mostly concentrated in the Western States.  83 of the 1,234 peaks (7%) were East of the Mississippi.  Two peaks (the high points of the Black Hills and the Ozark Mtns.) are in the Midwest states.  The remainder (93%) are in 11 western states plus West Texas.

TABLE 5:  TOP 10 STATES BY NUMBER OF P>2000 SUMMITS

5.2    Prominence Density

Dividing the number of prominences into the surface area of the state yields its prominence density. This measure would appear to make Washington the "most mountainous" state in the country.

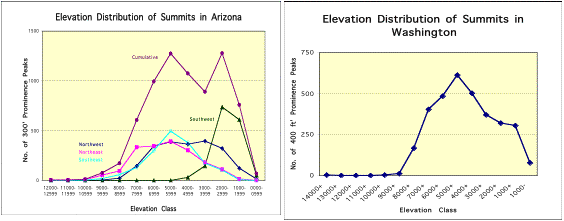
5.3        Lognormal distribution of datasets

How is prominence distributed across the terrain manifold?  A robust quantitative analysis is hampered by a lack of clean data sets.  With the completion of the U.S. P2000 dataset, as well as lists for Great Britain (to P500') and partial lists for Arizona (to P=300) and Washington (to P=400), the natural distribution of summits is beginning to show form.  A statistically significant sampling of P>300' summits will help us begin to understand how scale dependent is the distribution of mountains.

TABLE 9:          
DISTRIBUTION OF 500' PROMINENCES IN THE UK AND IRELAND
List courtesy of Richard Webb and Alan Dawson.

P Value        No. of Peaks

4,000+                   1
3,000-3,999             11
2,000-2,999            100
1,000-1,999            397
500-999               1037

As more data becomes available, the relevant question will be how the distribution of prominence varies by physiographic terrain type.  Are summits distributed similarly in highly glaciated alpine terrains such as the North Cascades as they are in well-weathered low elevation landscapes, such as the Eastern U.S. and Great Britain?

While the above datasets would appear to provide us with good ratios to predict the worldwide distribution of mountains, attempts at  simple predictions thus far have mostly resulted in a high level of inaccuracy. Two observations:

1.    The persistence of ultra-prominent i.e. P>5,000' summits worldwide has been a poor indicator of the distribution of lower prominence summits.  Physi regions often have a certain modularity to their highest elevations (for example the absence of any summits above 5,000' on Britain provides no indication of the number of P>500' hills to expect.)  Even in instances where there is a statistically significant number of ultra-prominences, distribution curves appear to differ greatly.  The high Karakorum has, not surprisingly, a great density of 5,000' prominences but not the related number of P2000s and P300s that one might statistically predict.

2.    Lists of the most prominent summits tend to be skewed by the number and height modularity of island and volcano high points.  Islands, particularly volcanic ones, often have one high prominence peak and few sub peaks relative to the continental ultras.  The existence of 12 ultra-prominent summits in the Aleutian chain might predict that there will be 3,480 P>500' hills.  In fact there are probably about 200.

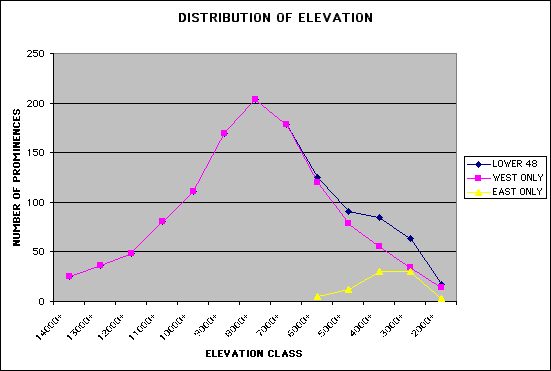
5.4.               Prominence and elevation

I took the 1,234 peak dataset and looked at their distribution of elevation.  Mountains appear to be well distributed across the 1,000' elevation intervals in an almost perfect bell-curve. 

The data (in blue) shows a slight lognormal bias to the right (lower elevations).  If we remove the Eastern U.S. data points (in yellow), which form a discrete branch of the divide tree, this bias is entirely corrected.

For the United States dataset, the mean elevation is 8,246', and the median is 8,312'.  For the Western U.S. only (1,154 summits), the mean elevation is 8,519', and the median is 8,482' - an insignificant difference.

Is the distribution of mountains terrain dependent; i.e. do different geomorphological processes affect the statistical occurrence of mountain summits?  Since we tend to equate low prominence summits (hills) with lower elevations, a natural assumption would be that as the prominence cutoff were lowered, the distribution curve would shift to the right, but this is not borne out by the data thus far.

There are possible mathematical explanations for the distribution of mountains.  Normal bell-curves can be formed by the aggregation of many smaller bell-curves.  Since different geographical regions, that represent discrete branches of the divide tree, have different elevation modularities, their aggregation may tend to smooth out these differences.  On the other hand,  elevation in the United States is not randomly distributed, leading us to wonder if the measurement of prominence tends to adjust for these differences. 

Another explanation is that a divide tree has a tendency towards symmetry.  An elevation cross-section might on average have the same number of summits on each side of the central divide.  The map of the United States does not seem to bear this out:  more than 80% of the data points are west of the continental divide for example.  However symmetry in the aggregate might help explain the evenness of mountain distribution.  

The following datasets are inconclusive, both are based on arbitrary political divisions and do not reflect a natural branch of the divide tree:

1.      A list of Washington state prominences compiled by Jeff Howbert.  The set of 4,000+ summits is 90% complete, missing some hills in the east of the state.

2.     A list of summits to P300 for Arizona, by Bob Martin and Mark Nichols.  Unfortunately this data contains two large biases that are difficult to compensate.   The list includes named summits with P<300'.  The more significant limitation is that Indian Reservations and Military Bases were not included on the list (which was made for hikers, not for statistical purposes), which creates holes in the divide tree in presumably specific elevation ranges.

5.5         Dominance

A mountain's prominence value divided by total elevation is one indication of the degree to which a summit stands out.  Eberhard Jurgalski proposes the term 'dominance'.

The highpoint of a sea island or natural continent would have 100% dominance (elevation equals prominence.)  Some other summits, notably in California and Washington appear to be virtual land islands, rising on every side above a coastal plain.  In Europe, Mont Blanc is 99% dominant.

Of the 1,234 P2,000 summits, 251 (20%) have more than 50% dominance.  26 (2%) have more than 80% dominance.  The following list of 13 summits have  >90% dominance.

Lassen Peak coincidentally has exactly 50% dominance.  The mountain elevation is 10,457', and its Key Saddle (Beckwourth Pass) is half way at 5,228'.