Section 8: Lineage Groups and

Mountain Hierarchies

We demonstrated that prominence, lineage areas, and domains are non-arbitrary functions of the elevation of terrain. Lineage Cells on the other hand are scale-specific functions.

8.1 Three Types of Parent and Three Types of Set-Theory

Just as there is no "natural parent" of a summit there is no perfect definition of its domain. The three types of parents can each be applied to our understanding of lineages and areas, creating a simple matrix of definitions.

PARENT RELATIONSHIPS AND GROUPS	Height-Derived	Height-Derived plus Prominence	Height-Derived plus Prominence plus Proportionality
Point (Parent)	Line Parent (NHN): Entirely scale dependent definition of parent but works well for two reasons: Allows us to build a lineage key with a given dataset. Always points us in the right direction across the key saddle. Fewest constraints.	Prominence Parent (PP): Non-scale dependent definition of parent, but has some limitation. Requires calculation of the parent prominence, which is somewhat unrelated to the mountain in question. IE, the Parent of Whitney requires measurement of Orizaba, not of Whitney itself. Additional constraints.	Island Parent (IP): Non-scale dependent system works well in some cases (measuring sub-peaks on a major mountain) but is irrelevant in other cases (continental systems.)
Line (Lineage)	Lineage is based on NHN rule: A line of successively higher summits all the way to the island or continental high point. Only constraint is the scale at which low-prominence peaks are included.	Lineage based on PP rule only: A line of successively more prominent summits. Interesting if the notion is to identify successively greater and greater peaks. Robin Tivy named this the PromLine.	Lineage based on IP rule only: A matrushka doll nesting philosophy of mountains. Gets to the continental high point pretty quickly. Limited usefulness.
Area (Orometric Group)	Lineage Area: The region of land that counts the summit in the lineage. Size of area unfortunately poorly correlated to importance of the mountain. Fewest constraints system for building cells.	PALA or Domain: Lineage Area adjusted for Prominence. By addition of one additional constraint, size of domain is now well-correlated with the importance of a mountain. Some peaks can still have huge domains depending on terrain, e.g. Pikes Peak extending to Mississippi River.	"Prominence Island" Groupings: Not directly analogous. It is possible to draw nested domains based on island parents. Works OK at large scales, but becomes fairly irrelevant at the continental scale.

8.2 The Group Mentality

Having now covered the basic concepts of Lineage Theory, we can have a little fun with the grouping of mountains into hierarchies.

The treatment of mountain hierarchies, like cladistics in taxonomy, is a combination of rules and judgment. Strict adherence to a single qualifying rule (such as the Prominence Island groupings above) would yield an unsatsifactory result.

The Cell Map treatment is somewhat satisfactory at a large scale, such as P=2,000' or greater. For my purposes, I tend to use simple "cell-division" rules, as described in the previous section, for mapping at P2000 or larger.

Some judgment should be employed at smaller scales in order to come up with cells that are proportionate in size and importance. This is because ultra-prominences are not very evenly distributed at a continental scale. One would not ascribe the same level of importance to a group of 2,000 sq. mi. in British Columbia as to the entire Eastern United States, based simply on the presence of an ultra-prominent summit.

In order to divide the world into Orometric Groups, I therefore employ a simple three-tier system of hierarchy. This complements the work being done by researchers at www.bivouac.com.

The first-tier is a rough division of the montane regions of the continent. In the case of North America, this results in 17 continental divisions (plus a few groupings of islands.)

The second-tier is roughly analogous to the 5,000' prominence cutoff, except that judgment has been used to conbine and separate regions based on distinctive physiographic attributes. The result is that mountainous areas are broken into regions roughly as large as a medium-sized state.

The third-tier defaults to the simple cell structure of the P2000s. In mountainous states, this yields a satisfactory consistent size that allows for the classification of smaller hills by P2000 parent. In eastern states such as West Virginia (one P2000) or Kentucky and Pennsylvania (zero P2000s), a lower cutoff would obviously have to be employed for the third-tier. In any respect, it is felt that a standard prominence value suffices at this scale.

8.3 First Order Groupings: Disecting the continent

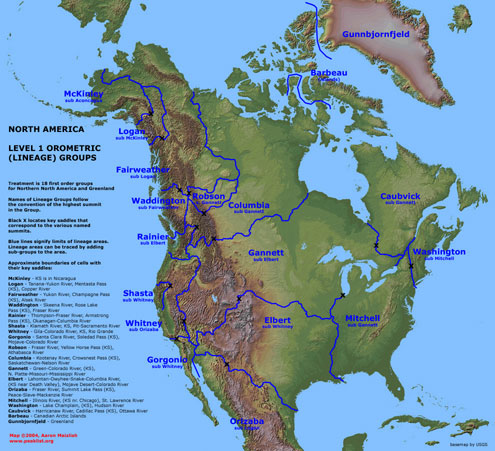I divided North America into 17 continental regions, as demonstrated in the map :

FULL SIZE IMAGE

The regions are:

Continental:

McKinley
Logan
Fairweather
Waddington
Robson
Columbia
Rainier
Gannett
Elbert
Whitney
Gorgonio
Caubvick
Washington
Mitchell
Orizaba
Tajamulco (not shown)
Chirippo (not shown)

Islands:

Barbeau (Canadian Arctic)
Gunnbjornfjeld (Greenland)
Duarte (Caribbean)

In each case, the named summit is the highest point in the group. The summit does not have to be the most prominent point in the group (lower more prominent peaks are allowed) but in each of the North American cases they are also most prominent.

On the map I showed the "parent" of each group summit. In this case the parent is merely the group to which the lineage of each group directs, it is not necessarily the PP or IP of the summit.

8.4 Second Order Groupings: Approximating the Ultra Level

(I'll write some text about it someday.. in the meantime, a lot of my ideas were nicely incorporated into the bivouac.com mountain hierarchy system, which you might want to have a look at.)

California 2nd Order Groupings
Arizona 2nd Order Groupings

8.5 Third Order Groupings: The P2000 Lineage Cells

(text to follow someday)

California Lineage Cells

Forward to Page 9

Back to Table of Contents

Back to Theory Page