| Back to Table of Contents | Back to Theory Page | Forward
to Page 8 |
At the beginning of this essay we posed the paradox that mountain summits exist as a fixed point on the terrain (x,y,z coordinates) but that the mountain as a large object is a fuzzy notion without definable boundaries. Later we noted that J. C. Maxwell wrote that hills are bounded by watercourses in the same manner that dales are bounded by watersheds. This implied that hills can be described with definite boundaries, albeit in a sort of static, cellular fashion. Prominence, Line Parents and lineage all suggest that there is a non-static hierarchy of mountains, and this allows us to investigate the natural areal extent of mountains.
Starting with
Maxwell's
observation, we can take any set of summits, say every hill over
P=2000'
on a
given divide tree, and outline the boundaries that separate each of
them. We start by identifying every key
saddle and then trace the two unique slope lines (on the channel tree)
that
descend from
them. We continue until each of
these watercourses either merge, reach a pit or reach the ocean.
When our line reaches a pit we find
its corresponding basin saddle and repeat the process.
The resulting map would be a sort of
flat, non-hierarchical segmentation of all of the land into discrete
provinces. I call this method a Lineage
Cell map. It forms the basis for group theory in the next
section.
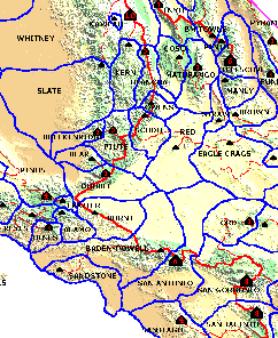
Unfortunately, a Lineage Cell map is somewhat limited in its use as it is entirely scale dependent. The "province" assigned to each summit is purely a function of the prominence cutoff employed (P>2000' in our example).
Figure 10.1 is a
detail of an
experimental P2000 Lineage Cell map of California.
By changing the
prominence cutoff, we could create fewer cells or more cells.
Cells with a low prominence cutoff are always subsets of
cells with a high prominence cutoff.
The one thing that a lineage cell map tells us is that the summit is always the highest point in the selected cell, and is also the only point of prominence X in that cell, where X equals the minimum cutoff value. In the map below, one could say that the summit is the first point of P2,000 in the lineage of every point within that cell.
FIGURE 10.1: Sample
Lineage Cell Map (P=2,000')

Just as every summit has a unique string of summits (the lineage) that connect it to the continental highpoint, so too does that summit have a unique set of points that include it in their lineage. That set of points can be neatly described as a Lineage Area.
Lineage Area is computed as follows: For a given summit, identify the Key Saddle and ALSO every secondary saddle that connects it to all higher summits (as indicated earlier, more than half of summits are terminal summits with only the key saddle). From this set of saddles, trace the watercourses (channel lines) until they either merge or reach the ocean. It can be demonstrated that every point of terrain inside this region counts our summit in its lineage.
A map of the lineage areas for Loma Prieta (E=3,786, P=3,426) and Mount Diablo (E=3,849, P=3,109), two major Bay Area summits, is shown below. Note that they are both terminal summits.
Copernicus Peak (E=4,372, P=3,092), the highest mountain in the region, is also a terminal summit. The lineage areas of Diablo and Loma Prieta are subsets of the lineage area of Copernicus Peak. Diablo and Loma Prieta are both lower peaks with greater prominence.
Looking back at Table 10, there are 45 P>300' summits that lead from downtown San Francisco to Aconcagua. San Francisco is in the lineage area of each of these 45 summits. Each of the 45 lineage areas are a superset of the previous summit lineage area and a subset of the following lineage area.
Figure 10.3 shows a
detail of the
Mt. Piños (Ventura County, CA) Lineage Area.
Two
saddles demarcate the boundary of the Piños lineage area, the
Piños key saddle (Tehachapi Pass) and the San Gorgonio key
saddle
(Soledad
Pass). They represent the two
critical paths from Piños to higher ground.
These channel lines merge after a sequence of enclosed basins to
the east of the two
saddles. In fact three of the four
watercourses that emerge from Piños' saddles never reach the
ocean. That
is not a rare occurrence in the arid West. For example all of the
slope lines that originate at the summit of Mt. Whitney end in pits -
precipitation falling on Whitney's summit never reaches the ocean as
surface water by natural
means.
| Figure 10.2 |
Figure
10.3 |
| Lineage Areas for Loma Prieta and Mt. Diablo | Detail of Lineage Area for Mt. Piños
(eastern) |
|
|
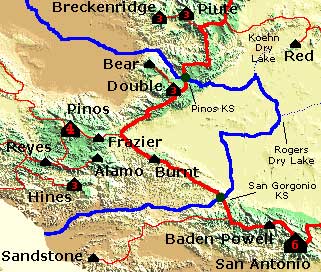 |
The Piños lineage area includes all of the coast ranges to the west of this map as far north as San Francisco Bay. By definition, Piños is the high point of this area. In one sense, the Lineage Area is the outer extent of the flanks of a mountain. By employing the NHN rule, we were able to get past the sense of arbitrariness derived from Maxwell's individual cells for individual hills, and built a sort of "system-with-fewest-constraints" that describes a fundamental relationship between summit and surrounding terrain.
Lineage Area produces an unfortunate result that I call the "Langley problem." Mt. Langley is a high Sierra summit (E=14,028, P=1,167) just south of Mt. Whitney, which is also on the San Francisco lineage chart. As a subpeak of an ultra-prominence (Whitney), and as a terminal summit, it is also a part of the lineage for all summits from San Francisco south to the tip of Baja California, a lineage area of approximately 150,000 square miles. So its lineage area far exceeds the importance that one would expect to ascribe such a minor summit. While one may grasp that San Francisco and Cabo San Lucas are both on the "flanks" of Mt. Whitney in a manner of speaking, the same statement for Mt. Langley stretches the imagination. Thus, lineage area is not a perfect fit for conceptualizing the natural area of a summit. Fortunately prominence helps us address this perceptual problem.
Mt. Langley's lineage area is disproportionate to its prominence because it is a subpeak near a high prominence mountain. But if we take the lineage area of Langley, and remove from it all lineage areas of higher-prominence, lower-elevation peaks, we are left with a non-arbitrary region that is proportionate to Langley's prominence. This "solves" the Langley problem.
I call this a Prominence Adjusted Lineage Area, or PALA. Peter Ridges, a British prominence enthusiast, refers to the PALA as a Domain. A domain feels like the very natural area ascribable to a mountain.
Computation of a PALA is similar to a lineage area, except that the secondary saddles includes the set of all saddles that connect the peak to more prominent summits, whether higher or lower. A PALA is always a subset of the Lineage Area; they never have overlapping boundaries.
In the frequent instance where a terminal summit is also the most prominent summit in its lineage area, such as with Mt. Diablo and Loma Prieta, the PALA is equal to the lineage area. Copernicus Peak on the other hand has these two lower-elevation higher-prominence peaks in its lineage area, whose areas are thus excluded from its PALA. Mt. Langley's PALA is about 250 sq. mi.
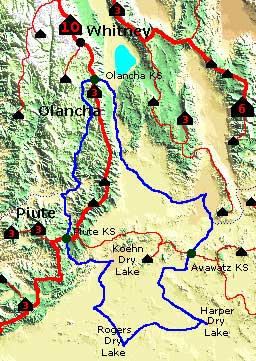
Figure 10.4 shows the PALA for Olancha Peak, that high Sierra summit that was the NHN to San Gorgonio. Olancha, like Langley, is a terminal summit, with only a key saddle connecting it to Langley and Whitney. Its lineage area is virtually the same as Mt. Langley, encompassing approximately 150,000 square miles of Central and Southern California and all of Baja California.
Note that the Olancha PALA has three qualifying saddles (green circles on the map). They are the Olancha key saddle, and also the key saddles for Piute Peak and Avawatz Mtn, both of which are lower and more prominent. This domain is ±2,500 sq. mi., including a lengthy section of the Sierra Crest and some high desert. The outline of this PALA is also discernable on the Lineage Cell map in Figure 10.1; where it comprises the combined Olancha, Owens, Scodie, and Red cells.
FIGURE 10.4 Olancha Peak PALA
 7.4.
Summit Groups
7.4.
Summit Groups In prominence theory, summits and the surface area that they represent tend to fall into natural clusters.
The most natural cluster is an entire branch of a divide. Branches that connect to the rest of the tree across one summit reflect a certain symmetry and topological consistency. Other natural groupings are the set of summits in a given lineage area or in a given PALA.
The Mount Piños PALA that we referred to in Figure 10.3 includes exactly 20 summits of P>2,000 and a few thousand summits of P>300'. Mountains could be ranked by the number of summits in their PALA; which would reflect a combination of a mountain's relative prominence and its centrality to the divide tree. Of course, lesser summits generally belong to many PALAs.
Lineage cells are the next-order derivative on summit groupings, and the only way to identify every summit by a unique grouping. All summits of P300' to P1,999' could be said to belong to exactly one lineage cell of P>2,000'. Forthcoming efforts to develop larger scale mapping of lesser summits will be based on their grouping in P=2,000' lineage cells.
Remember that all of
these
groupings of summits are a pure function of elevation, and do not
necessarily
correlate to their geomorphology.
Summits in a give mountain range will have a tendency to group
together
and be represented by their highest summit, but there are many
exceptions. Many
natural groups have outliers from other mountain ranges, such as the
desert
peaks that we saw attached to the Olancha PALA. Other
ranges are bisected by rivers, e.g. the Cascades and
the Wasatch Range, and therefore do not form a natural grouping of
summits derived
from the divide tree.
| Forward to Page 8 |
| Back to Table of Contents | Back to Theory Page |